[PID 튜토리얼] ①PID 제어란 무엇인가? / MATLAB 매트랩 / 예시 / PID 제어 하는법 / 비례제어 / 적분제어 / 크루즈 컨트롤

1. PID 제어란?

Proportional-Integral-Differential controller

쉽게 말해서 "비례 + 미분 + 적분" 제어기 입니다! 피드백을 통해 작동하는 제어기의 한 종류랍니다.

PID 제어는 드론, 로봇청소기, 자율주행 등 다양한 분야에서 사용하는데요, 한번 예시를 들어서 쉽게 이해해 봅시다~

2. 크루즈 컨트롤을 구현해보자🚗

비교적 간단한 예시인 "크루즈 컨트롤"을 이용해서 PID 제어를 이해해 봅시다.

크루즈 컨트롤이란 액셀을 밟지 않아도 차가 알아서 일정한 속도를 유지해 주는 기능을 말합니다.

우선, 크루즈 컨트롤을 적용할 차가 있어야겠죠?

고속도로에 시속 80km로 달리는 자동차가 있다고 상상해 보세요.

이 상태 그대로 액셀을 밟는 발을 조금 편하게 하기 위해서 크루즈 컨트롤을 시속 100km에 맞춰 보겠습니다~

가. On/Off control

조금은 원시적인(?) 방법으로, "속도가 느리면 풀악셀을 밟아라 / 빠르면 밟지 마라"

이런 식으로 속도를 제어할 수 있습니다. 상상 하는 것 만으로는 이해가 어려우니 구체화를 위해

"MATLAB" 을 사용해서 보여드릴게요.

(x축 시간[t], y축 속력 [v])

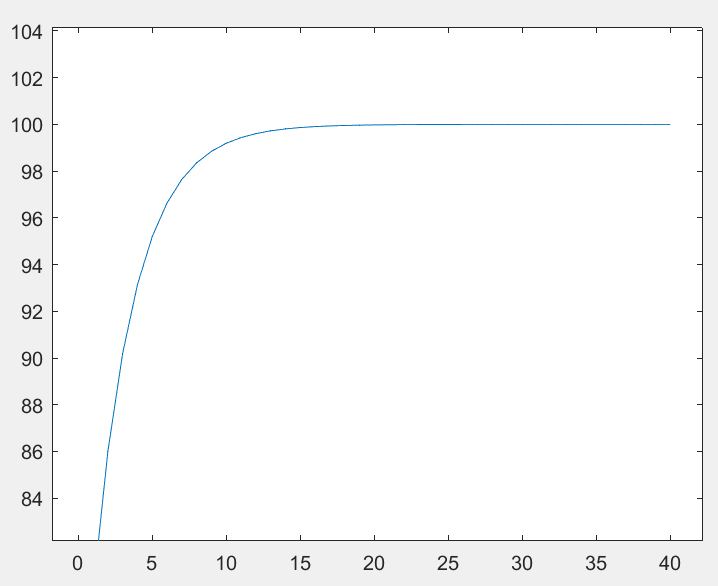
왼쪽의 간단한 매트랩 코드를 이용해서 On / Off 만으로 크루즈 컨트롤을 구현해 보았습니다.

그래프를 보면 시속 100km로 유지되지도 않고 보기만 해도 멀미가 날 것 같은 그런 속도 그래프가 나왔습니다.

이것이 바로 On/Off control의 한계점인데, 이것보다 더 발전되어서 이제 본격적으로 PID 컨트롤을 다뤄 보겠습니다!

궁금하다면 직접 MATLAB을 설치해 따라해 보세요.

https://kr.mathworks.com/products/matlab.html

MATLAB(매트랩) - 테크니컬 컴퓨팅 언어

MATLAB(매트랩) 소프트웨어 공식 홈페이지. MATLAB(매트랩)은 엔지니어 및 과학자를 위한 가장 쉽고도 생산적인 소프트웨어 환경입니다.

kr.mathworks.com

나. 비례 제어, Proportional control

비례 제어를 간단하게 설명하자면, 목표치(100km/h)와 현재 속도(v)의 편차에 비례하게 가속하는 것입니다.

목표와 차이가 클 때는 빠르게 가속하고, 목표치에 가까워질수록 점점 천천히 가속하게 된답니다.

이것을 매트랩으로 한번 구현해 볼게요~

위의 코드가 바로 비례 제어, Proportional control을 구현한 코드입니다! 이제 P, I, D 중에서 P를 구현했어요🎉

조금 더 정확하게 일반화된 식을 적어 보자면,

위 식처럼 되고요, e(t) 는 기준입력(r)과 측정된 출력(r_now)의 차로 간단하게 말하면 그냥 "오차"를 나타냅니다.
e(t) 앞의 Kp(제어 파라미터)는 적절한 값을 대입해야지 최상의 성능을 뽑아 낼 수 있답니다. 이 적절한 값을 찾아내는 과정을 "튜닝" 이라고 하고, Ziegler-Nichols 방법 등을 통해 실험적으로 찾아낼 수 있답니다.

그림5. (a) Kp가 작을 경우[0.07] (b) Kp가 조금 클 경우[1.77] (c) Kp가 매우 클 경우[2.2]

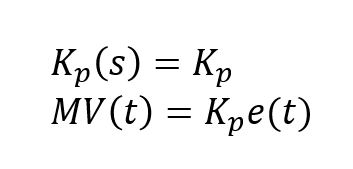
위 사진에서 보이듯이 Kp가 작을 경우 기준입력(r)에 도달하기까지 걸리는 시간이 길어집니다. (첫번째 사진)

Kp를 조금 더 키울 경우 두번째 사진처럼 비교적 빨리 기준입력(r)에 도달하기는 하지만, 불안정한 상태가 되고 기준입력(r) 주위에서 계속 진동하게 됩니다. 마지막 사진처럼 Kp가 너무 클 경우 오히려 발산해버리는 상태가 되기도 합니다.

이렇게 비례 제어(P)에는 단점이 존재합니다. 오차(e)는 점점 줄어들겠지만, 0이 되지 않고 점점 0과 비슷한 값으로 가까이 가기만 할 뿐이죠. 측정 출력(r_now)는 절대로 기준입력(r)에 도달하지 못합니다. 이 현상을 정상 상태 오차라고 하죠. 이런 점을 해결하기 위해서 바로 다음에 소개할 적분 제어(Integral control)을 사용한답니다~. 그렇다면 적분 제어를 알아볼까요?

다. 적분 제어, Integral control

적분항(I)를 수식으로 써 보면 위와 같이 쓸 수 있습니다. 파라미터 Ki에 0부터 t까지 오차(e)를 적분한 값을 곱해버립니다.

적분 제어는 주로 비례 제어에서 해결하지 못한 정상 상태 오차를 해결하는 역할을 해 줍니다.

이제 이것을 매트랩으로 어떻게 구현해야 할까요? 매트랩에서는 연속함수가 아닌, 정수 t에 대해서 배열로 제어값을 설정했기 때문에 다음과 같이 코드를 짤 수 있답니다.

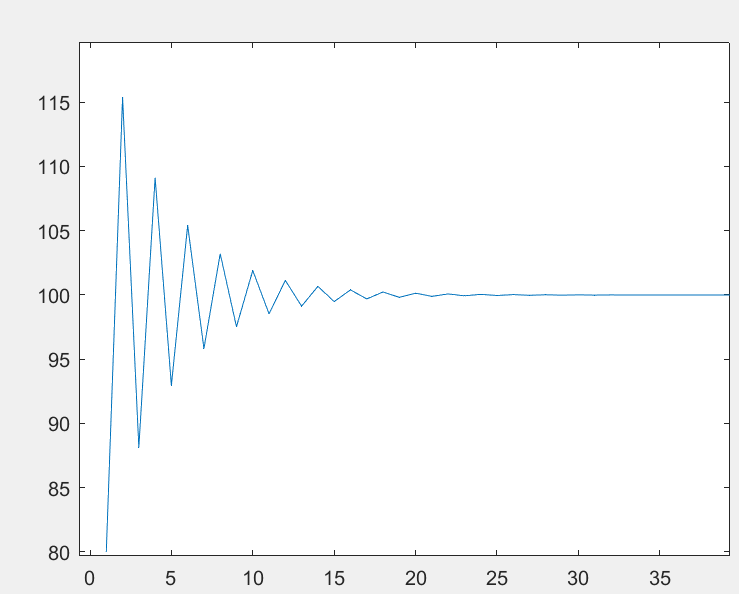
i라는 배열을 하나 더 만들고, 파라미터와 적절한 수를 오차에 곱해서 계속 더해주었어요. 일종의 적분과 비슷한 역할을 하겠죠? 오른쪽 그래프에서 보면 측정 출력(r_now)가 점점 100에 수렴하는 것을 볼 수 있습니다. 그와 더불어서, 기준입력까지 근접하는 시간인 상승시간이 확실히 줄어든 것을 볼 수 있죠. 이제 P와 I 까지 구현하게 되었네요 :)